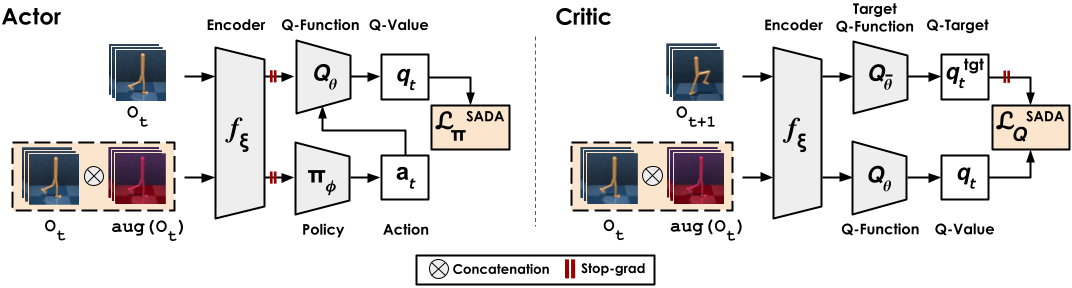
\(Q\)-learning algorithms are appealing for real-world applications due to their data-efficiency, but they are very prone to overfitting and training instabilities when trained from visual observations. Prior work, namely SVEA, finds that selective application of data augmentation can improve the visual generalization of RL agents without destabilizing training. We revisit its recipe for data augmentation, and find an assumption that limits its effectiveness to augmentations of a photometric nature. Addressing these limitations, we propose a generalized recipe, SADA, that works with wider varieties of augmentations. We benchmark its effectiveness on DMC-GB2 -- our proposed extension of the popular DMControl Generalization Benchmark -- as well as tasks from Meta-World and the Distracting Control Suite, and find that our method, SADA, greatly improves training stability and generalization of RL agents across a diverse set of augmentations.







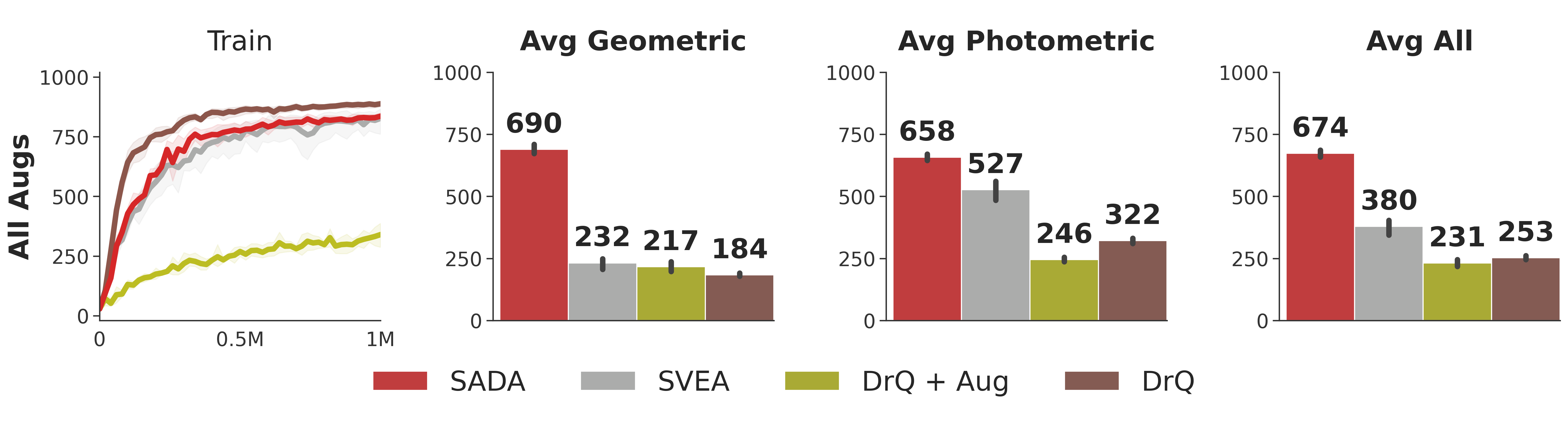 DMC-GB2 Overall Robustness. Episode reward on DMC-GB2 when trained under all (geometric and photometric) augmentations, averaged across all 6 DMControl tasks. Mean and 95% CI over 5 seeds.
Our method, SADA, displays superior robustness to diverse image transformation types, all while attaining a similar sample efficiency to its unaugmented
DrQ baseline in the training environment.
DMC-GB2 Overall Robustness. Episode reward on DMC-GB2 when trained under all (geometric and photometric) augmentations, averaged across all 6 DMControl tasks. Mean and 95% CI over 5 seeds.
Our method, SADA, displays superior robustness to diverse image transformation types, all while attaining a similar sample efficiency to its unaugmented
DrQ baseline in the training environment.
@article{almuzairee2024recipe,
title = {A Recipe for Unbounded Data Augmentation in Visual Reinforcement Learning},
author = {Almuzairee, Abdulaziz and Hansen, Nicklas and Christensen, Henrik I},
journal = {Reinforcement Learning Journal},
volume = {1},
pages = {130--157},
year = {2024},
}